Hdme

This paper describes the hdme R package, which provides implementation of variable selection in the presence of measurement error. Published in Journal of Open Source Software.

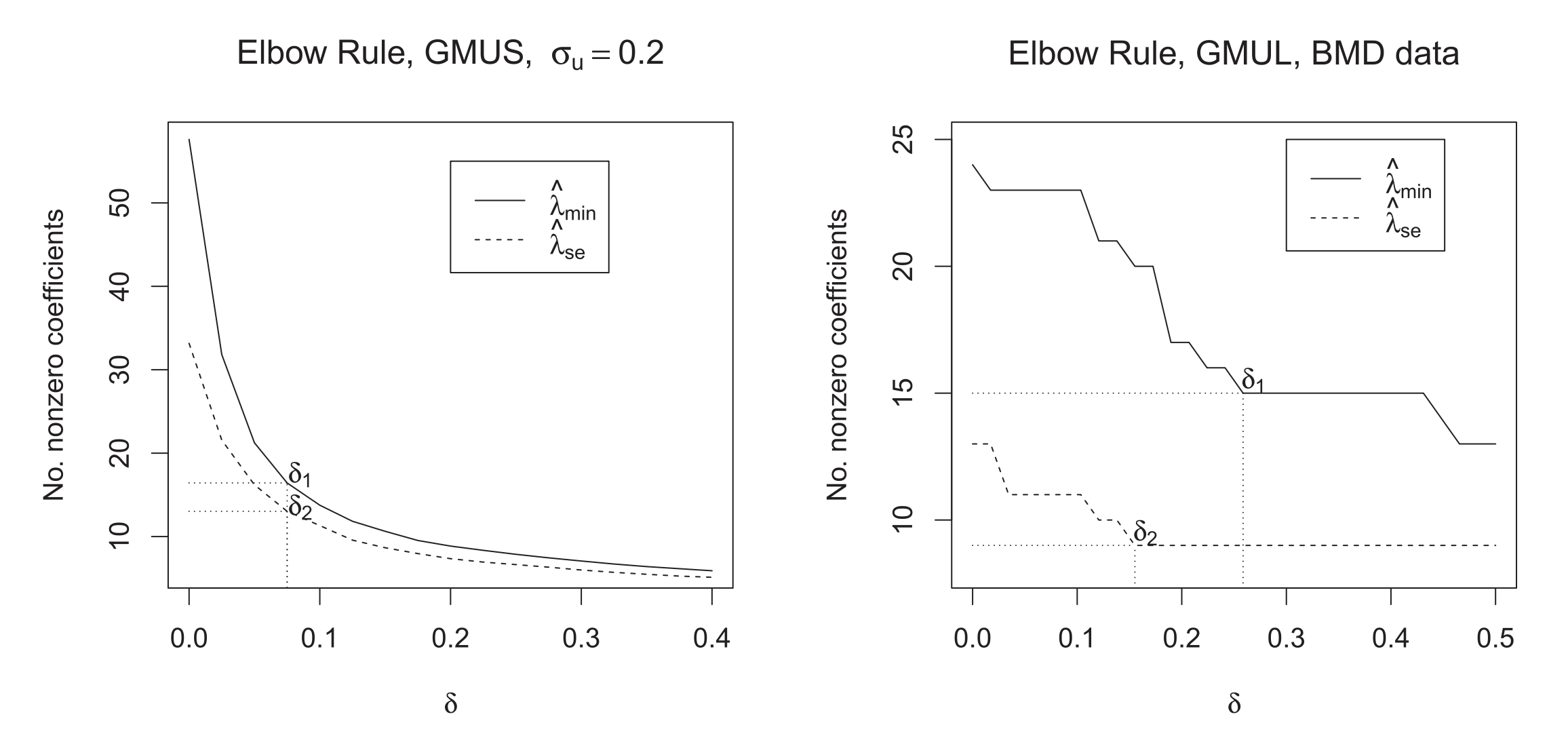
The matrix uncertainty selector is a modification of the Dantzig selector, for the case of variable selection with noisy predictors. In this paper we extend the matrix uncertainty selector to the generalized linear model case, and propose a computationally efficient computational algorithm. Compared to other methods that correct for the effect of measurement error, the matrix uncertainty selector and its extension do not require a precise estimate of the noise variance, which is an advantage in practical use. Published in Journal of Computational and Graphical Statistics.

This R package contains functions for fitting variable selection models in the presence of noise in the predictor variables. In particular, it supports a corrected lasso and the generalized matrix uncertainty selector. In addition, it offers an implementation of the (generalized) Dantzig selector.

This paper analyzes the impact of covariate measurement error in the lasso method for penalized regression. First, we present a result showing how the classical result for variable selection consistency breaks down in the presence of measurement error, and then we study a correction method and show how it recovers the consistent variable selection property. Finally, we consider an extension to logistic and Poisson regression. Published in Statistica Sinica.